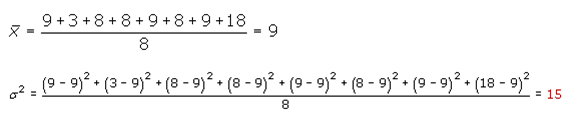Distribución de Probabilidad en las Ciencias de la Salud  En los servicios de salud, una de las interrogantes más comunes son: ¿Cuantos pacientes vendrán hoy a una hora determinada? ¿Cuál es la probabilidad de atender partos múltiples en un mes dado? ¿Cuál es la probabilidad de que un medicamento sea eficaz en un tratamiento dado? Todas estas interrogantes pueden ser contestadas en su mayoría, haciendo uso de las distribuciones de probabilidades Cuando se habla de los tipos de probabilidad, decimos que esta se clasifica en tres: 1.   Probabilidad clásica. 2.   Probabilidad distribución de frecuencias. 3.   Probabilidad subjetiva. La distribución de probabilidades está muy relacionada con el tipo de variables. Nosotros conocemos dos tipos de variables: a.   Variable discreta, y b.   Variable continúa. Una distribución de probabilidades para una variable aleatoria discreta es un listado mutuamente excluyente de todos los resultados numéricos posibles para esa variable aleatoria tal que una probabilidad específica de ocurrencia se asocia con cada resultado. El valor esperado de una variable aleatoria discreta es un promedio ponderado de todos los posibles resultados, donde las ponderaciones son las probabilidades asociadas con cada uno de los resultados. Donde: Xi = i-ésimo resultado de X, la variable discreta de interés. P(Xi) = probabilidad de ocurrencia del i-ésimo resultado de X La varianza de una variable aleatoria discreta (s 2) se define como el promedio ponderado de los cuadros de las diferencias entre cada resultado posible y su media (los pesos son las probabilidades de los resultados posibles).   Dónde: Xi = i-ésimo resultado de X, la variable discreta de interés. P(Xi) = probabilidad de ocurrencia del i-ésimo resultado de X Las distribuciones de probabilidades discretas más importantes son: 1.   Distribución Binomial, y 2.   Distribución de Poisson DISTRIBUCION BINOMIAL La distribución binomial es una distribución de probabilidades que surge al cumplirse cinco condiciones: 1.   Existe una serie de N ensayos, 2.   En cada ensayo hay sólo dos posibles resultados, 3.   En cada ensayo, los dos resultados posibles son mutuamente excluyentes, 4.   Los resultados de cada ensayo son independientes entre si, y 5.   La probabilidad de cada resultado posible en cualquier ensayo es la misma de un ensayo a otro. Cuando se cumple estas condiciones, la distribución binomial proporciona cada resultado posible de los N ensayos y la probabilidad de obtener cada uno de estos resultados. Para este tipo de distribución de probabilidad, la función matemática es la siguiente: Donde: P(X) = probabilidad de X éxitos dados los parámetros n y p n = tamaño de la muestra p = probabilidad de éxito 1 – p = probabilidad de fracaso X = numero de éxitos en la muestra ( X = 0, 1, 2, …….. n) El término indica la probabilidad de obtener X éxitos de n observaciones en una secuencia específica. En término indica cuantas combinaciones de los X éxitos entre n observaciones son posibles. Entonces dado el número de observaciones n y la probabilidad de éxito p, la probabilidad de X éxitos es: P(X) = (numero de de secuencia posibles) x (probabilidad de un secuencia especifica) Por eso que llegamos a la función matemática que representa esta distribución. Ejemplo

Un laboratorio afirma que una droga causa efectos secundarios en una proporción de 3 de cada 100 pacientes. Para contrastar esta afirmación, otro laboratorio elige al azar a 5 pacientes a los que aplica la droga. ¿Cuál es la probabilidad de los siguientes sucesos?

1. Ningún paciente tenga efectos secundarios
2. Al menos dos tengan efectos secundarios
3. ¿Cuál es el número medio de pacientes que espera laboratorio que sufran efectos secundarios si elige 100 pacientes al azar?

Esperanza Matemática

En Bioestadística la esperanza matemática también llamada esperanza, valor esperado, media poblacional o media de una variable aleatoria , es el número  que formaliza la idea de valor medio de un fenómeno aleatorio.

Cuando la variable aleatoria es discreta, la esperanza es igual a la suma de la probabilidad de cada posible suceso aleatorio multiplicado por el valor de dicho suceso. Por lo tanto, representa la cantidad media que se "espera" como resultado de un experimento aleatorio cuando la probabilidad de cada suceso se mantiene constante y el experimento se repite un elevado número de veces. Cabe decir que el valor que toma la esperanza matemática en algunos casos puede no ser "esperado" en el sentido más general de la palabra - el valor de la esperanza puede ser improbable o incluso imposible.

La esperanza matemática tiene las siguientes propiedades principales:

1. E(x) al igual que la media, es un número que depende de todos los valores de la serie y de sus respectivas probabilidades, ya que todos ellos entran en su cálculo.

2. Si  X  e  Y  son variables aleatorias, entonces

     E (X + Y) = E(X) + E(Y)
    E(Ax) = A E(x)
    E(X.Y) = E(X) E(Y)
    E(X₁ + X₂ +.........+ X_e) = E(X₁)+ E(X₂) +.........+ E(X_e)
    E(X₁ + X₂ +.........+ X_t) = E(X₁) E(X₂) *.........* E(X_t)
     E(X + a) = E(X) + a
     E(ax + b) = aE(X) + b

3. Si “ A ” es una constante y “ X ” una variable, 

4. Si X e Y son variables aleatorias independientes 

5. Si X₁, X₂, ......., X_e son variables aleatorias

6. Si X₁, X₂, ......., X_t son variables aleatorias independientes

7. La esperanza matemática es un valor que oscila en el intervalo (Mínimo X_i; máximo X_i), en donde, tiende a situarse en el     centro, para así considerarse representativa de los valores de la serie de datos.

8. Si “ X ” es variable aleatoria y “ a ” una constante ,

9. Sea X una variable aleatoria , “ a ” y “ b”constantes,

• El valor esperado cuando tiramos un dado equilibrado de 6 caras es 3,5. y cabe destacar que 3,5 no es un valor posible al rodar el dado. En este caso, en el que todos los sucesos son de igual probabilidad, la esperanza es igual a la media aritmetica.

• Una aplicación común de la esperanza matemática es en las apuestas o los juegos de azar. Por ejemplo, la ruleta americana tiene 38 casillas equiprobables. La ganancia para acertar una apuesta a un solo número paga de 35 a 1 (es decir, cobramos 35 veces lo que hemos apostado y recuperamos la apuesta, así que recibimos 36 veces lo que hemos apostado). Por tanto, considerando los 38 posibles resultados, la esperanza matemática del beneficio para apostar a un solo número es: -0,0526 aproximadamente. Por lo tanto uno esperaría, en media, perder unos 5 céntimos por cada euro que apuesta, y el valor esperado para apostar 1 euro son 0.9474 euros. En el mundo de las apuestas, un juego donde el beneficio esperado es cero (no ganamos ni perdemos) se llama un "juego justo".

La varianza Se puede definir como el "casi promedio" de los cuadrados de las desviaciones de los datos con respecto a la media muestral.  Propiedades de la varianza  Dos propiedades importantes de la varianza son: 1.    La varianza de una constante es cero 2.    Otra propiedad importante es que si se tiene la varianza  de de un conjunto de datos y a cada observación se multiplica por una constante, entonces la nueva varianza de los datos se obtiene multiplicando a la varianza de los datos por . Ejemplo  Calcular la varianza de la distribución:

9, 3, 8, 8, 9, 8, 9, 18

La desviación típica o desviación estándar  Denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos,  es una medida de dispersión para variables de razón (variables cuantitativas o cantidades racionales) y de intervalo. Se define como la raíz cuadrada de la varianza de la variable. La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio). Propiedades de la desviación estándar 1 La desviación estándar será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales. 2 Si a todos los valores de la variable se les suma un número la desviación estándar no varía. 3 Si todos los valores de la variable se multiplican por un número la desviación estándar queda multiplicada por dicho número. 4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones estándar se puede calcular la desviación estándar total. Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes: 12, 6, 7, 3, 15, 10, 18, 5. Por ejemplo, las tres muestras (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, 8) cada una tiene una media de 7. Sus desviaciones estándar muestrales son 7, 4 y 1 respectivamente. La tercera muestra tiene una desviación mucho menor que las otras dos porque sus valores están más cerca de 7.

Cómo contribuyen las estadísticas a mejorar la salud

Los países necesitan estadísticas sanitarias para saber por qué mueren las personas o cuáles son las causas de enfermedades y traumatismos más comunes en la población. Armados con esta información, los países pueden abordar los problemas de salud y priorizar el uso de recursos sanitarios muy valiosos.

Cada año, la OMS analiza los datos de sus 193 Estados Miembros y elabora estimaciones de carga de morbilidad y mortalidad que se publican en el informe Estadísticas Sanitarias Mundiales. Dichas estimaciones vienen a ser como la boleta de calificaciones de la salud mundial.

Cómo recoge la OMS sus estadísticas

Las estadísticas de la OMS provienen de innumerables fuentes y se obtienen aplicando diversos métodos, como son las encuestas domiciliarias, los informes sistemáticos presentados por los servicios de salud, el registro civil, los censos de población y los sistemas de vigilancia epidemiológica.

Problema

La obesidad puede definirse como la acumulación excesiva de grasa en el organismo, que puede llegar a constituir un serio peligro para la salud. La causa subyacente en un balance energético positivo, que tiene como consecuencia el aumento de peso, es decir, que las calorías consumidas exceden las calorías que se gastan.

¿Qué trastornos causa la obesidad?

 La acumulación excesiva de grasa en el cuerpo puede llegar a constituir un serio peligro para la salud. Adicionalmente, a los trastornos físicos que puede ocasionar la obesidad, hay que sumarles los problemas psicológicos provocados por la discriminación social y las dificultades para relacionarse con los demás que sufre una persona cuya figura desborda los límites de la silueta saludable. Además, en la infancia el problema puede ser aún mayor por la angustia que provoca en el niño la cruel discriminación de los compañeros del colegio y amigos.

¿Cuándo se considera que un niño es obeso?

Un niño se considera que es obeso cuando su peso sobrepasa el 20% de su peso ideal. La probabilidad de ser un adulto obeso cuando se ha sido un niño obeso es diferente según la edad de comienzo de dicha obesidad, siendo del 40% cuando la obesidad comienza entre los 6 meses y los 7 años de vida, y del 70% para los que comenzaron con obesidad entre los 10 y los 13 años. Esta diferencia se explica por que las células que almacenan grasa se multiplican sobre todo en esta etapa de la vida (de 10 a 13 años).

El índice de masa corporal (IMC), medido al menos una vez al año, es una buena manera de diagnosticar el desarrollo de la obesidad en un niño. El IMC tiene la ventaja de contabilizar tanto la altura como el peso del individuo. En la práctica, señala si un niño está ganando demasiado peso para su altura, o si es equilibrado.

 

Si se sufre de obesidad, se  tiene más probabilidades de tener concentraciones anormales de grasas en la sangre, es decir, de tener concentraciones altas de triglicéridos y de colesterol LDL (colesterol "malo") y concentraciones bajas de colesterol HDL (colesterol "bueno").

Personas con sobrepeso, posee el síndrome metabólico, el cual es el nombre con que se conoce un conjunto de factores de riesgo que aumentan las probabilidades de sufrir enfermedad coronaria y otros problemas de salud, como diabetes y accidente cerebrovascular (derrame cerebral).

Se diagnostica el síndrome metabólico si se presentan por lo menos tres de los siguientes factores de riesgo:

• Medida grande de la circunferencia de la cintura. Esta situación se llama obesidad abdominal o de "tipo manzana". El exceso de grasa en la zona de la cintura eleva más el riesgo de sufrir enfermedad de las arterias coronarias que si el exceso de grasa estuviera en otras partes del cuerpo, por ejemplo, en las caderas.
• Concentración de triglicéridos más alta de lo normal (o el hecho de estar tomando medicinas para controlar los triglicéridos altos).
• Concentración de colesterol HDL más baja de lo normal (o el hecho de estar tomando medicinas para controlar el colesterol HDL bajo).
• Presión arterial más alta de lo normal (o el hecho de estar tomando medicinas para controlar la presión arterial alta).
• Concentración de glucosa sanguínea en ayunas más alta de lo normal (o el hecho de estar tomando medicinas para el tratamiento de la diabetes).

Relación de la Probabilidad con la Ciencia de la Salud

La probabilidad es la posibilidad de que algo ocurra.  Las probabilidades se expresan como fracciones o como  decimales que están entre uno y cero.

• ·       Tener una probabilidad de cero significa que algo nunca va a suceder.
• ·       Una probabilidad de uno indica que algo va a suceder siempre.

La probabilidad, en relación con las ciencias de la salud, mide la frecuencia con la que ocurre un resultado, para sacar conclusiones acerca de experimentos realizados, como el estudio de la eficacia de los fármacos y el aclara miento de los factores de riesgo de los mismos.

Entender las probabilidades es fundamental para el proceso de toma de decisiones en el área de salud.

La teoría de probabilidades también permite al médico extraer conclusiones acerca de una población de pacientes, basado en la información acerca de una muestra de los mismos extraída de esa población.

Este proceso se denomina inferencia estadística.

Desde esta perspectiva, los profesionales de la salud siempre buscan lo mejor para sus pacientes. Así que necesitan una información clara, verdadera y justificada que los guie por el camino correcto, al momento de escoger el mejor tratamiento para una enfermedad, reconocer los síntomas característicos de patologías, para así encontrarles cura e identificar el porqué de las enfermedades.

La probabilidad es un elemento indispensable para los profesionales, asimismo permite, no solo tener fundamentos lógicos y creíbles acerca de enfermedades, fármacos, diagnósticos, sino también que nos sirve para llevar un control de enfermedades contagiosas y a la vez prevenirlas.

Todo esto se logra gracias al uso de la probabilidad, porque siendo un método que nos permite analizar datos verdaderos, que se obtienen de un riguroso proceso de estudio comparativo y podemos escoger lo mejor para los pacientes, satisfaciendo sus necesidades.
La importancia de la probabilidad en el ejercicio de los profesionales de la salud, es porque gracias a ella, se puede tener certeza y seguridad de la credibilidad del trabajo arduo que desempeñan, así pues la probabilidad es importante de modo que ha servido en el estudio de enfermedades crónicas y terminales como el sida, cáncer y otras.

Por otra parte la probabilidad ha evitado muchas muertes y desastres en todos los campos de las ciencias de la salud, así mismo como participan en el diario vivir de todos los profesionales de este campo, para hacerlos excelentes en su trabajo.

Ejemplos

• ·     Un médico afirma que un paciente X tiene una oportunidad de  50% de sobrevivir a una operación; o que un paciente Y tiene  80% de posibilidades de tener una enfermedad particular.
• 
  
• ·   Una fuente autorizada del Ministerio de Salud; declara a la  prensa de que este verano hay 1% de posibilidades de que se desate una epidemia de cólera en la Capital.

Aunque el resultado de ninguna prueba es absolutamente exacto, eso no afecta la probabilidad de la presencia o ausencia de una enfermedad.