En Bioestadística la esperanza
matemática también llamada esperanza, valor esperado, media
poblacional o media de una variable aleatoria , es el
número que
formaliza la idea de valor medio de un fenómeno aleatorio.
La esperanza matemática tiene las siguientes propiedades principales:
1. E(x) al igual que la media, es un
número que depende de todos los valores de la serie y de sus respectivas probabilidades,
ya que todos ellos entran en su cálculo.
2. Si X e Y son variables
aleatorias, entonces
E (X + Y) = E(X) + E(Y)
E(Ax) = A E(x)
E(X.Y) = E(X) E(Y)
E(X1 + X2 +.........+ Xe) = E(X1)+ E(X2) +.........+ E(Xe)
E(X1 + X2 +.........+ Xt) = E(X1) E(X2) *.........* E(Xt)
E(X + a) = E(X) + a
E(ax + b) = aE(X) + b
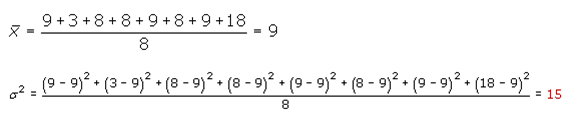
E (X + Y) = E(X) + E(Y)
E(Ax) = A E(x)
E(X.Y) = E(X) E(Y)
E(X1 + X2 +.........+ Xe) = E(X1)+ E(X2) +.........+ E(Xe)
E(X1 + X2 +.........+ Xt) = E(X1) E(X2) *.........* E(Xt)
E(X + a) = E(X) + a
E(ax + b) = aE(X) + b
3. Si “ A ” es una constante y “ X ” una variable,
4. Si X e Y son variables aleatorias independientes
5. Si X1, X2, ......., Xe son variables aleatorias
6. Si X1, X2, ......., Xt son variables aleatorias independientes
7. La esperanza matemática es un valor que oscila en el intervalo (Mínimo Xi; máximo Xi), en donde, tiende a situarse en el centro, para así considerarse representativa de los valores de la serie de datos.
8. Si “ X ” es variable aleatoria y “ a ” una constante ,
9. Sea X una variable aleatoria , “ a ” y “ b”constantes,
- El valor esperado cuando tiramos un dado equilibrado de 6 caras es 3,5. y cabe destacar que 3,5 no es un valor posible al rodar el dado. En este caso, en el que todos los sucesos son de igual probabilidad, la esperanza es igual a la media aritmetica.
- Una aplicación común de la esperanza matemática es en las apuestas o los juegos de azar. Por ejemplo, la ruleta americana tiene 38 casillas equiprobables. La ganancia para acertar una apuesta a un solo número paga de 35 a 1 (es decir, cobramos 35 veces lo que hemos apostado y recuperamos la apuesta, así que recibimos 36 veces lo que hemos apostado). Por tanto, considerando los 38 posibles resultados, la esperanza matemática del beneficio para apostar a un solo número es: -0,0526 aproximadamente. Por lo tanto uno esperaría, en media, perder unos 5 céntimos por cada euro que apuesta, y el valor esperado para apostar 1 euro son 0.9474 euros. En el mundo de las apuestas, un juego donde el beneficio esperado es cero (no ganamos ni perdemos) se llama un "juego justo".
La
varianza
Se puede definir como el "casi
promedio" de los cuadrados de las desviaciones de los datos con respecto
a la media muestral.
Propiedades de la varianza
Dos propiedades importantes de la varianza son:
1. La varianza de una constante es cero
Ejemplo
Calcular la varianza de la distribución:
|
9, 3, 8, 8, 9, 8, 9, 18
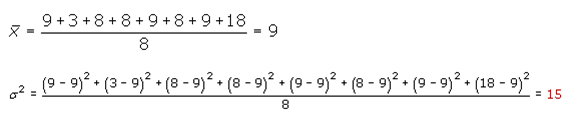

No hay comentarios.:
Publicar un comentario