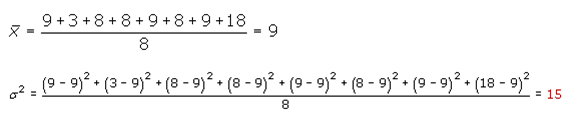Distribución de Probabilidad en las Ciencias de la Salud  En los servicios de salud, una de las interrogantes más comunes son: ¿Cuantos pacientes vendrán hoy a una hora determinada? ¿Cuál es la probabilidad de atender partos múltiples en un mes dado? ¿Cuál es la probabilidad de que un medicamento sea eficaz en un tratamiento dado? Todas estas interrogantes pueden ser contestadas en su mayoría, haciendo uso de las distribuciones de probabilidades Cuando se habla de los tipos de probabilidad, decimos que esta se clasifica en tres: 1.   Probabilidad clásica. 2.   Probabilidad distribución de frecuencias. 3.   Probabilidad subjetiva. La distribución de probabilidades está muy relacionada con el tipo de variables. Nosotros conocemos dos tipos de variables: a.   Variable discreta, y b.   Variable continúa. Una distribución de probabilidades para una variable aleatoria discreta es un listado mutuamente excluyente de todos los resultados numéricos posibles para esa variable aleatoria tal que una probabilidad específica de ocurrencia se asocia con cada resultado. El valor esperado de una variable aleatoria discreta es un promedio ponderado de todos los posibles resultados, donde las ponderaciones son las probabilidades asociadas con cada uno de los resultados. Donde: Xi = i-ésimo resultado de X, la variable discreta de interés. P(Xi) = probabilidad de ocurrencia del i-ésimo resultado de X La varianza de una variable aleatoria discreta (s 2) se define como el promedio ponderado de los cuadros de las diferencias entre cada resultado posible y su media (los pesos son las probabilidades de los resultados posibles).   Dónde: Xi = i-ésimo resultado de X, la variable discreta de interés. P(Xi) = probabilidad de ocurrencia del i-ésimo resultado de X Las distribuciones de probabilidades discretas más importantes son: 1.   Distribución Binomial, y 2.   Distribución de Poisson DISTRIBUCION BINOMIAL La distribución binomial es una distribución de probabilidades que surge al cumplirse cinco condiciones: 1.   Existe una serie de N ensayos, 2.   En cada ensayo hay sólo dos posibles resultados, 3.   En cada ensayo, los dos resultados posibles son mutuamente excluyentes, 4.   Los resultados de cada ensayo son independientes entre si, y 5.   La probabilidad de cada resultado posible en cualquier ensayo es la misma de un ensayo a otro. Cuando se cumple estas condiciones, la distribución binomial proporciona cada resultado posible de los N ensayos y la probabilidad de obtener cada uno de estos resultados. Para este tipo de distribución de probabilidad, la función matemática es la siguiente: Donde: P(X) = probabilidad de X éxitos dados los parámetros n y p n = tamaño de la muestra p = probabilidad de éxito 1 – p = probabilidad de fracaso X = numero de éxitos en la muestra ( X = 0, 1, 2, …….. n) El término indica la probabilidad de obtener X éxitos de n observaciones en una secuencia específica. En término indica cuantas combinaciones de los X éxitos entre n observaciones son posibles. Entonces dado el número de observaciones n y la probabilidad de éxito p, la probabilidad de X éxitos es: P(X) = (numero de de secuencia posibles) x (probabilidad de un secuencia especifica) Por eso que llegamos a la función matemática que representa esta distribución. Ejemplo

Un laboratorio afirma que una droga causa efectos secundarios en una proporción de 3 de cada 100 pacientes. Para contrastar esta afirmación, otro laboratorio elige al azar a 5 pacientes a los que aplica la droga. ¿Cuál es la probabilidad de los siguientes sucesos?

1. Ningún paciente tenga efectos secundarios
2. Al menos dos tengan efectos secundarios
3. ¿Cuál es el número medio de pacientes que espera laboratorio que sufran efectos secundarios si elige 100 pacientes al azar?

Esperanza Matemática

En Bioestadística la esperanza matemática también llamada esperanza, valor esperado, media poblacional o media de una variable aleatoria , es el número  que formaliza la idea de valor medio de un fenómeno aleatorio.

Cuando la variable aleatoria es discreta, la esperanza es igual a la suma de la probabilidad de cada posible suceso aleatorio multiplicado por el valor de dicho suceso. Por lo tanto, representa la cantidad media que se "espera" como resultado de un experimento aleatorio cuando la probabilidad de cada suceso se mantiene constante y el experimento se repite un elevado número de veces. Cabe decir que el valor que toma la esperanza matemática en algunos casos puede no ser "esperado" en el sentido más general de la palabra - el valor de la esperanza puede ser improbable o incluso imposible.

La esperanza matemática tiene las siguientes propiedades principales:

1. E(x) al igual que la media, es un número que depende de todos los valores de la serie y de sus respectivas probabilidades, ya que todos ellos entran en su cálculo.

2. Si  X  e  Y  son variables aleatorias, entonces

     E (X + Y) = E(X) + E(Y)
    E(Ax) = A E(x)
    E(X.Y) = E(X) E(Y)
    E(X₁ + X₂ +.........+ X_e) = E(X₁)+ E(X₂) +.........+ E(X_e)
    E(X₁ + X₂ +.........+ X_t) = E(X₁) E(X₂) *.........* E(X_t)
     E(X + a) = E(X) + a
     E(ax + b) = aE(X) + b

3. Si “ A ” es una constante y “ X ” una variable, 

4. Si X e Y son variables aleatorias independientes 

5. Si X₁, X₂, ......., X_e son variables aleatorias

6. Si X₁, X₂, ......., X_t son variables aleatorias independientes

7. La esperanza matemática es un valor que oscila en el intervalo (Mínimo X_i; máximo X_i), en donde, tiende a situarse en el     centro, para así considerarse representativa de los valores de la serie de datos.

8. Si “ X ” es variable aleatoria y “ a ” una constante ,

9. Sea X una variable aleatoria , “ a ” y “ b”constantes,

• El valor esperado cuando tiramos un dado equilibrado de 6 caras es 3,5. y cabe destacar que 3,5 no es un valor posible al rodar el dado. En este caso, en el que todos los sucesos son de igual probabilidad, la esperanza es igual a la media aritmetica.

• Una aplicación común de la esperanza matemática es en las apuestas o los juegos de azar. Por ejemplo, la ruleta americana tiene 38 casillas equiprobables. La ganancia para acertar una apuesta a un solo número paga de 35 a 1 (es decir, cobramos 35 veces lo que hemos apostado y recuperamos la apuesta, así que recibimos 36 veces lo que hemos apostado). Por tanto, considerando los 38 posibles resultados, la esperanza matemática del beneficio para apostar a un solo número es: -0,0526 aproximadamente. Por lo tanto uno esperaría, en media, perder unos 5 céntimos por cada euro que apuesta, y el valor esperado para apostar 1 euro son 0.9474 euros. En el mundo de las apuestas, un juego donde el beneficio esperado es cero (no ganamos ni perdemos) se llama un "juego justo".

La varianza Se puede definir como el "casi promedio" de los cuadrados de las desviaciones de los datos con respecto a la media muestral.  Propiedades de la varianza  Dos propiedades importantes de la varianza son: 1.    La varianza de una constante es cero 2.    Otra propiedad importante es que si se tiene la varianza  de de un conjunto de datos y a cada observación se multiplica por una constante, entonces la nueva varianza de los datos se obtiene multiplicando a la varianza de los datos por . Ejemplo  Calcular la varianza de la distribución:

9, 3, 8, 8, 9, 8, 9, 18

La desviación típica o desviación estándar  Denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos,  es una medida de dispersión para variables de razón (variables cuantitativas o cantidades racionales) y de intervalo. Se define como la raíz cuadrada de la varianza de la variable. La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio). Propiedades de la desviación estándar 1 La desviación estándar será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales. 2 Si a todos los valores de la variable se les suma un número la desviación estándar no varía. 3 Si todos los valores de la variable se multiplican por un número la desviación estándar queda multiplicada por dicho número. 4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones estándar se puede calcular la desviación estándar total. Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes: 12, 6, 7, 3, 15, 10, 18, 5. Por ejemplo, las tres muestras (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, 8) cada una tiene una media de 7. Sus desviaciones estándar muestrales son 7, 4 y 1 respectivamente. La tercera muestra tiene una desviación mucho menor que las otras dos porque sus valores están más cerca de 7.